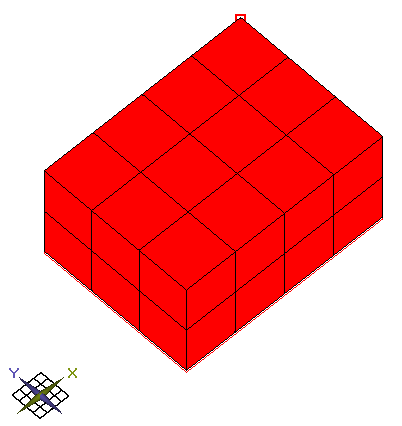
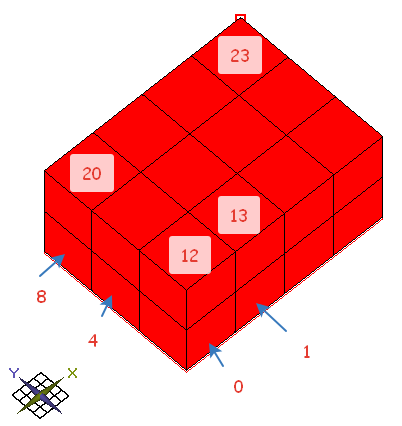
There is a block model
X axis – 4 blocks
Y axis – 3 blocks
Z axis – 2 blocks
Overall: 24 blocks.
Let’s number the blocks
How many the shortest paths are there between block [0] and [23]?
How long the shortest path? The length is 6 steps = 3 steps by X axis + 2 steps by Y axis and 1 step by Z axis.
The number of paths is a number of permutation with repetition = 6! / (3!*2!*1!) = 720 / (6*2*1) = 60
Another way to calc the number of paths is to create a graph and adjacency matrix.
Then we should multiply the matrix by itself 6 times and we get a number of paths of length of 6 steps between vertices.
Here we get interesting conclusion – if number of paths that are got by both two methods is equal, then the block model has all 24 blocks.